Data-Mining for Processes in Chemistry, Materials, and Engineering

Hao Li

Zhien Zhang

Zhien Zhang

2,* and

Zhe-Ze Zhao

Zhe-Ze Zhao

College of Chemistry, Sichuan University, Chengdu 610064, China

William G. Lowrie Department of Chemical and Biomolecular Engineering, The Ohio State University, 151 West Woodruff Avenue, Columbus, OH 43210, USA

School of Life Sciences and State Key Laboratory of Agrobiotechnology, The Chinese University of Hong Kong, Shatin, New Territories, Hong Kong, China

Authors to whom correspondence should be addressed.

Current Address: Department of Chemistry and the Institute for Computational and Engineering Sciences, The University of Texas at Austin, 105 E. 24th Street, Stop A5300, Austin, TX 78712, USA.

Processes 2019, 7(3), 151; https://doi.org/10.3390/pr7030151

Submission received: 11 February 2019 / Revised: 2 March 2019 / Accepted: 4 March 2019 / Published: 11 March 2019

(This article belongs to the Special Issue Process Modelling and Simulation)

Abstract

With the rapid development of machine learning techniques, data-mining for processes in chemistry, materials, and engineering has been widely reported in recent years. In this discussion, we summarize some typical applications for process optimization, design, and evaluation of chemistry, materials, and engineering. Although the research and application targets are various, many important common points still exist in their data-mining. We then propose a generalized strategy based on the philosophy of data-mining, which should be applicable for the design and optimization targets for processes in various fields with both scientific and industrial purposes.

1. Introduction

Data-mining is a strategy for discovering intrinsic relationships and making proper predictions based on statistics from scientifically-collected data [1]. With the rapid progress in machine learning techniques and methodologies in the recent decade [2,3,4,5,6,7], data-mining has become a popular study since machine learning provides an efficient technique for non-linearly fitting the intrinsic relationships between the independent and dependent variables in a mathematical form. Therefore, without knowing the exact physical or empirical form of the relationships among data, machine learning can come up with a non-linear form of math that could precisely predict the trends of data, including interpolation and extrapolation [8,9,10]. Although those non-linear forms do not contain the exact correlation knowledge, a general approximation of data-based machine learning (with both supervised and unsupervised processes [11,12,13]) always shows precise prediction and could address the problem in an easier way.

In recent years, data-mining has been widely applied for solving problems in chemical, materials, and engineering processes, based on the data collected from either experiments or simulations [14,15,16,17]. In many worldwide pressing issues, such as greenhouse gas capture [18,19], catalytic materials design and optimization [20,21,22,23,24,25,26,27,28,29,30,31], and renewable energy studies [32,33,34,35,36,37,38,39], data-mining has shown predictive power for mining the relationships between the intrinsic and extrinsic properties [40,41,42,43,44,45]. Usually, the mission of a data-mining process is to predict (or output) those variables that are difficult to acquire from experiments/simulations by using the easy variables which can be acquired as the inputs. Through a well-fitted non-linear form, the predicted variables can be rapidly outputted with the inputs of those independent variables. In other words, a machine learning assisted data-mining process is able to expedite the (i) optimization of engineering processes, (ii) discovery of new functional materials, and (iii) understanding of chemical processes.

Despite a number of studies that have been published in the recent decade, there is no well-established philosophy that provides a standard guideline for doing data-mining. Therefore, in this discussion paper, we are motivated to summarize some recent typical studies of data-mining in the processes of chemistry, materials, and engineering. Based on the brief review, comments, and discussions, we then generalize a simple but useful data-mining strategy for these scientific and application processes, which should ultimately benefit to the standard development of knowledge-based data-mining through a machine learning modeling process.

2. Typical Studies

Due to the high-dimensional variables, trends in the chemical processes are sometimes difficult to understand and predict. For example, a chemical process usually depends on multiple factors, including temperature, pressure, as well as the component and composition of reactants. Previously, to capture the relationships between these independent and dependent factors, a response surface methodology (RSM) was usually applied to fit the trends between the independent and dependent variables with multiple 3-D plots [46]. This method is useful for the design and optimization of chemical and materials processes. However, RSM is only able to deal with very limited independent variables in one model, which is not applicable for higher dimension problems in a big-data scale. To address this issue, artificial neural networks (ANNs), as the most widely used machine learning algorithms, have been applied for the same target, replacing RSM [8,47]. People have found that not only being able to deal with high-dimension problems ANNs also have a generalized approximation capacity and tunable algorithmic architectures, which guarantees that they can exhaustively capture the potential relationships between inputs and output(s) after a proper data training and validation process.

Mining the Trends and Properties in Chemistry and Materials

A typical application for mining the trends and properties in a chemical process is the greenhouse gas capture and utilization. In our recent study, it was found that a kernel-based ANN, the general regression neural network (GRNN), is able to properly fit the relationships between the solution properties (temperature, operating gas pressure, component, and concentration of the blended solutions) and the solubility of CO2, based on the literature-extracted experimental data [48]. Afterwards, the trends of CO2 solubility can be predicted with the function of temperature, operating CO2 pressure, concentration, and type of blended solutions (Figure 1). It can be seen from Figure 1 that though the trends are non-linear and usually difficult to be predicted with regular non-linear mathematical forms, a GRNN model trained from representative experimental data is able to capture these trends and provide proper understandings for CO2 capture in solutions. A similar study on predicting CO2 thermodynamic properties is shown in Reference [49], where the inputs of blend concentration, temperature, and CO2 operating partial pressure can be used as inputs and specifically predict the CO2 solubility, density, and viscosity of a solution. Similar studies for mining the gas capture and separation can be found in References [50,51]. In addition to the use of ANNs, Günay et al. used a decision tree model to evaluate the important factors of the reaction activity and selectivity of catalysts during CO2 electro-reduction process (Figure 2) [52]. By extracting a large number of experimental literatures, they classified the catalysts with the best Faradaic efficiency, max activity, or most selective pathway. Other catalytic applications through data-mining can be found in References [53,54]. Since most of the chemical and reaction-related processes are based on temperature, pressure, component, composition, and energetic values, it is expected that the data-mining strategy shown here is general and should be applicable for addressing other similar chemical issues through machine learning.

In terms of mining the materials properties, one of the most typical works is the discovery of nature’s missing ternary oxide compounds, as described by Ceder et al. [55]. They developed a machine learning model based on the crystal structure database and suggested new compositions and structures through a data-mining process. Then, using density function theory (DFT) as the quantum mechanical computation method [56,57], they calculated and confirmed the stability of those suggested ternary oxides (Figure 3). Similar studies can be found in recent References [58,59,60,61]. Due to the complexity of the structural information and the electronic structures of the periodic table elements [62,63,64,65,66,67,68,69,70,71], a challenge of their data-mining is the definition of suitable descriptors as the model inputs. In the past decades, there was a large number of descriptors that have been applied for the machine learning process of chemical and materials systems, such as bond length, bond angle, and group contribution analysis [72]. However, since the structural information is usually dependent on the coordination and reference, it was hard to generalize the methods for more complicated systems. To address these issues and provide a generalized machine learning representation, Behler and Parrinello developed a set of new symmetry functions that converts all the atomistic environments into the terms of pair and angular interactions [73]. Together with an architecture of conventional ANN, the relationship between the atomistic structures and the materials properties (e.g., energy) can be efficiently mined. So far, this Behler-Parrinello representation has proven to be highly effective for capturing the structural information of materials during machine learning, which especially benefits to the data-mining in theoretical chemistry and computational materials based on quantum mechanical calculated data.

3. Processes in Engineering

3.1. Engineering Optimization and Design

Engineering process is somewhat different from the processes of chemistry and materials discussed above. The main reason is that most of the knowledge in engineering are based on various empirical equations, due to the complexity of the systems. Therefore, mining the intrinsic relationships during engineering processes are particularly challenging but also important. A typical study using data-mining method for the optimization and design of engineering applications is proposed by Kalogirou [74], where an ANN was applied to train a small number of data from TRNSYS simulations on a typical solar energy system for industrial engineering. Then, a genetic algorithm (GA) [75,76,77] was employed to estimate the optimum size of parameters based on the results from ANN. Interestingly, the use of GA has shown a promising process that could generate reliable data combinations in a short time (Figure 4). Instead of listing the interpolated trends as discussed above, the GA method is a fast way that could expedites the industrial decision on the processes.

3.2. A Computational High-Throughput Screenig Method

Though a GA method is sufficient for generating a limited amount of data, its strategy sometimes would omit the important possible parameters during design. In addition, being different from materials design (as shown in Figure 3), engineering applications require to operate a larger size of data since the materials types are limited by the finite number of elements. And thus, there are many more different possibilities exist in the design and optimization of engineering processes. To overcome these problems, in very recent years, a high-throughput screening (HTS) method was developed for optimizing the engineering devices and processes (Figure 5) [78,79]. As illustrated in Figure 5, it can be seen that an HTS method can generate a large number of possible combination of inputs at the beginning, then a well-trained ANN can rapidly output the performance of all these possible input combinations. Then all those combinations which predicted with good performance would be recorded in a database as future candidates. Then the experimental process can pick a few of these candidates for testing. In previous studies, it has been shown that a regular ANN (trained with 1~2 hidden layers, respectively, with less than 50 hidden neurons) is able to quickly output thousands of predictions in a relatively short period [78]. More importantly, an HTS method is able to fully mine the trends between input and output variables for engineering processes.

4. Discussions

With the case analysis discussed above, we can see that a machine learning assisted data-mining is a powerful technique for fitting the intrinsic relationships in the processes of chemistry, materials, and engineering. In addition, it is clear that there are a couple of important steps for these data-mining. First, the choice of model inputs is important since it should be the independent variables that have potential relationships with the output variable(s). Therefore, the use of descriptors should be carefully selected. Second, since the predictions are usually for interpolation, the database used for machine learning model training should be sufficiently representative and diverse. Otherwise, the model might easily get over-fitted [80]. Finally, for prediction, optimization, and/or design applications, the way to generate new combined input data could be carefully chosen: for new materials design, the combination of different types of elements from the periodic table is a good way to screen all the possible materials which are predicted with high-performances; for targeting a good design with less computational cost, a GA method could help to rationally generate new input combinations; to exhaustively screen all the possible optimization in engineering, an HTS method could be a good strategy since the prediction through an already-trained machine learning (e.g., ANN) model is usually computationally costless [78].

Overall, the general data-mining process remains similar regardless of its applications, as summarized in Figure 6. After data collection, a statistical analysis would evaluate whether the data scale is diverse and representative. Then the most reasonable independent variables can be chosen as the descriptors in the model inputs. By training and validation of the machine learning model, we can evaluate whether the descriptors are suitable for capturing the potential relationships with the output(s). If the model is well-trained, it can be used for further mining of the new properties by performing its predictive power. Those new input combinations generated by GA or HTS can be set as the input of the trained model, and the predictions can be rapidly outputted. Finally, a new database can be constructed by having the original experimental data as well as the predicted data from the well-trained machine learning model.

5. Conclusions

In the new era of machine learning development, data-mining for processes in chemistry, materials, and engineering has become a popular way to promote efficiency in both scientific and industrial research. In this discussion, we have summarized several typical cases for the optimization and design of chemistry, materials, engineering, and other related applications. We found that though there is a variety of research and application fields, the basic strategy, process, and philosophy of data-mining are highly similar. We then have proposed a generalized strategy for the basic philosophy of data-mining, which should be applicable for the design and optimization targets for the processes in various fields. We also expect that in future studies with larger data-scale in science and industry, some more advanced machine learning (e.g., deep learning) techniques could fulfill the future requirement of data-mining, leading to faster and more efficient scientific development.

Author Contributions

Both H.L. and Z.Z. wrote this discussion paper. Z.-Z.Z. provided important insights in the discussion of the paper.

Funding

This research received no external funding.

Acknowledgments

We are grateful for all the editorial works from the Processes editorial office.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Wu, X.; Kumar, V.; Ross Quinlan, J.; Ghosh, J.; Yang, Q.; Motoda, H.; McLachlan, G.J.; Ng, A.; Liu, B.; Yu, P.S.; et al. Top 10 algorithms in data mining. Knowl. Inf. Syst. 2008, 14 , 1–37. [Google Scholar] [CrossRef]
  2. Goh, K.L.; Singh, A.K. Comprehensive Literature Review on Machine Learning Structures for Web Spam Classification. Procedia Comput. Sci. 2015, 70 , 434–441. [Google Scholar] [CrossRef] [Green Version]
  3. Sattlecker, M.; Stone, N.; Bessant, C. Current trends in machine-learning methods applied to spectroscopic cancer diagnosis. TrAC Trends Anal. Chem. 2014, 59 , 17–25. [Google Scholar] [CrossRef]
  4. Schmidhuber, J. Deep Learning in neural networks: An overview. Neural Netw. 2015, 61 , 85–117. [Google Scholar] [CrossRef] [PubMed]
  5. Kotsiantis, S.B. Supervised Machine Learning: A Review of Classification Techniques. Informatica 2007, 31 , 249–268. [Google Scholar] [CrossRef]
  6. Lin, J.; Yuan, J.-S. Analysis and Simulation of Capacitor-Less ReRAM-Based Stochastic Neurons for the in-Memory Spiking Neural Network. IEEE Trans. Biomed. Circuits Syst. 2018, 12 , 1004–1017. [Google Scholar] [CrossRef] [PubMed]
  7. Lin, J.; Yuan, J. Capacitor-less RRAM-Based Stochastic Neuron for Event-Based Unsupervised Learning. In Proceedings of the 2017 IEEE Biomedical Circuits and Systems Conference (BioCAS), Turin, Italy, 19–21 October 2017. [Google Scholar]
  8. Li, H.; Zhang, Z.; Liu, Z. Application of Artificial Neural Networks for Catalysis: A Review. Catalysts 2017, 7 , 306. [Google Scholar] [CrossRef]
  9. Li, H.; Chen, F.; Cheng, K.; Zhao, Z.; Yang, D. Prediction of Zeta Potential of Decomposed Peat via Machine Learning: Comparative Study of Support Vector Machine and Artificial Neural Networks. Int. J. Electrochem. Sci. 2015, 10 , 6044–6056. [Google Scholar]
  10. Li, H.; Tang, X.; Wang, R.; Lin, F.; Liu, Z.; Cheng, K. Comparative Study on Theoretical and Machine Learning Methods for Acquiring Compressed Liquid Densities of 1,1,1,2,3,3,3-Heptafluoropropane (R227ea) via Song and Mason Equation, Support Vector Machine, and Artificial Neural Networks. Appl. Sci. 2016, 6 , 25. [Google Scholar] [CrossRef]
  11. Kawamoto, Y.; Takagi, H.; Nishiyama, H.; Kato, N. Efficient Resource Allocation Utilizing Q-Learning in Multiple UA Communications. IEEE Trans. Netw. Sci. Eng. 2018. [Google Scholar] [CrossRef]
  12. Siniscalchi, S.M.; Salerno, V.M. Adaptation to new microphones using artificial neural networks with trainable activation functions. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28 , 1959–1965. [Google Scholar] [CrossRef] [PubMed]
  13. Hofmann, T. Unsupervised learning by probabilistic Latent Semantic Analysis. Mach. Learn. 2001, 42 , 77–196. [Google Scholar] [CrossRef]
  14. Witten, I.H.; Frank, E. Data Mining: Practical Machine Learning Tools and Techniques ; Morgan Kaufmann: Boston, MA, USA, 2005. [Google Scholar]
  15. Wu, H.; Yu, Y.; Fu, H.; Zhang, L. On the prediction of chemical exergy of organic substances using least square support vector machine. Energy Sources Part A Recover. Util. Environ. Eff. 2017, 39 , 2210–2215. [Google Scholar] [CrossRef]
  16. Wu, K.; Liu, D.; Tang, Y. In-situ single-step chemical synthesis of graphene-decorated CoFe2O4composite with enhanced Li ion storage behaviors. Electrochim. Acta 2018, 263 , 515–523. [Google Scholar] [CrossRef]
  17. Wu, K.; Du, K.; Hu, G. Red-blood-cell-like (NH4)[Fe2(OH)(PO4)2]•2H2O particles: Fabrication and application in high-performance LiFePO4 cathode materials. J. Mater. Chem. A 2018, 6 , 1057–1066. [Google Scholar] [CrossRef]
  18. Zhang, Z.; Li, Y.; Zhang, W.; Wang, J.; Soltanian, M.R.; Olabi, A.G. Effectiveness of amino acid salt solutions in capturing CO2: A review. Renew. Sustain. Energy Rev. 2018, 98 , 179–188. [Google Scholar] [CrossRef]
  19. Song, J.; Feng, Q.; Wang, X.; Fu, H.; Jiang, W.; Chen, B.; Song, J.; Feng, Q.; Wang, X.; Fu, H.; et al. Spatial Association and Effect Evaluation of CO2 Emission in the Chengdu-Chongqing Urban Agglomeration: Quantitative Evidence from Social Network Analysis. Sustainability 2018, 11 , 1. [Google Scholar] [CrossRef]
  20. Li, H.; Henkelman, G. Dehydrogenation Selectivity of Ethanol on Close-Packed Transition Metal Surfaces: A Computational Study of Monometallic, Pd/Au, and Rh/Au Catalysts. J. Phys. Chem. C 2017, 121 , 27504–27510. [Google Scholar] [CrossRef]
  21. Li, H.; Evans, E.J.; Mullins, C.B.; Henkelman, G. Ethanol Decomposition on Pd–Au Alloy Catalysts. J. Phys. Chem. C 2018, 122 , 22024–22032. [Google Scholar] [CrossRef]
  22. Wu, K.; Yang, H.; Jia, L.; Pan, Y.; Hao, Y.; Zhang, K.; Du, K.; Hu, G. Smart construction of 3D N-doped graphene honeycombs with (NH4)2SO4 as a multifunctional template for Li-ion battery anode: “A choice that serves three purposes”. Green Chem. 2019. [Google Scholar] [CrossRef]
  23. Sun, Q.; Yang, Y.; Zhao, Z.; Zhang, Q.; Zhao, X.; Nie, G.; Jiao, T.; Peng, Q. Elaborate design of polymeric nanocomposites with Mg(ii)-buffering nanochannels for highly efficient and selective removal of heavy metals from water: Case study for Cu(ii). Environ. Sci. Nano 2018, 5 , 2440–2451. [Google Scholar] [CrossRef]
  24. Li, H.; Zhang, Z.; Liu, Y.; Cen, W.; Luo, X. Functional Group Effects on the HOMO–LUMO Gap of g-C3N. Nanomaterials 2018, 8 , 589. [Google Scholar] [CrossRef] [PubMed]
  25. Li, H.; Zhang, Z.; Liu, Z. Non-Monotonic Trends of Hydrogen Adsorption on Single Atom Doped g-C3N. Catalysts 2019, 9 , 84. [Google Scholar] [CrossRef]
  26. Yang, L.; Chen, Z.; Cui, D.; Luo, X.; Liang, B.; Yang, L.; Liu, T.; Wang, A.; Luo, S. Ultrafine palladium nanoparticles supported on 3D self-supported Ni foam for cathodic dechlorination of florfenicol. Chem. Eng. J. 2018, 359 , 894–901. [Google Scholar] [CrossRef]
  27. Shi, C.; He, Y.; Ding, M.; Wang, Y.; Zhong, J. Nanoimaging of food proteins by atomic force microscopy. Part II: Components, imaging modes, observation ways, and research types. Trends Food Sci. Technol. 2018. [Google Scholar] [CrossRef]
  28. Shi, C.; He, Y.; Ding, M.; Wang, Y.; Zhong, J. Nanoimaging of food proteins by atomic force microscopy. Part I: Components, imaging modes, observation ways, and research types. Trends Food Sci. Technol. 2018, 0–1. [Google Scholar] [CrossRef]
  29. Li, N.; Tang, S.; Rao, Y.; Qi, J.; Zhang, Q.; Yuan, D. Peroxymonosulfate enhanced antibiotic removal and synchronous electricity generation in a photocatalytic fuel cell. Electrochim. Acta 2019, 298 , 59–69. [Google Scholar] [CrossRef]
  30. Tang, S.; Yuan, D.; Rao, Y.; Li, M.; Shi, G.; Gu, J.; Zhang, T. Percarbonate promoted antibiotic decomposition in dielectric barrier discharge plasma. J. Hazard. Mater. 2019, 366 , 669–676. [Google Scholar] [CrossRef] [PubMed]
  31. Kang, L.; Du, H.L.; Du, X.; Wang, H.T.; Ma, W.L.; Wang, M.L.; Zhang, F.B. Study on dye wastewater treatment of tunable conductivity solid-waste-based composite cementitious material catalyst. Desalin. Water Treat. 2018, 125 , 296–301. [Google Scholar] [CrossRef]
  32. Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine learning methods for solar radiation forecasting: A review. Renew. Energy 2017, 105 , 569–582. [Google Scholar] [CrossRef]
  33. Liu, X.; He, Y.; Fu, H.; Chen, B.; Wang, M.; Wang, Z. How Environmental Protection Motivation Influences on Residents’ Recycled Water Reuse Behaviors: A Case Study in Xi’an City. Water 2018, 10 , 1282. [Google Scholar] [CrossRef]
  34. Liu, G.; Chen, B.; Jiang, S.; Fu, H.; Wang, L.; Jiang, W.; Liu, G.; Chen, B.; Jiang, S.; Fu, H.; et al. Double Entropy Joint Distribution Function and Its Application in Calculation of Design Wave Height. Entropy 2019, 21 , 64. [Google Scholar] [CrossRef]
  35. Wang, J.; Zhou, S.; Zhang, Z.; Yurchenko, D. High-performance piezoelectric wind energy harvester with Y-shaped attachments. Energy Convers. Manag. 2019, 181 , 645–652. [Google Scholar] [CrossRef]
  36. Wang, J.; Tang, L.; Zhao, L.; Zhang, Z. Efficiency investigation on energy harvesting from airflows in HVAC system based on galloping of isosceles triangle sectioned bluff bodies. Energy 2019, 172 , 1066–1078. [Google Scholar] [CrossRef]
  37. Yang, G.; Wang, J.; Zhang, H.; Jia, H.; Zhang, Y.; Gao, F. Applying bio-electric field of microbial fuel cell-upflow anaerobic sludge blanket reactor catalyzed blast furnace dusting ash for promoting anaerobic digestion. Water Res. 2019, 149 , 215–224. [Google Scholar] [CrossRef] [PubMed]
  38. Yu, L.; Li, Y.P. A flexible-possibilistic stochastic programming method for planning municipal-scale energy system through introducing renewable energies and electric vehicles. J. Clean. Prod. 2019, 207 , 772–787. [Google Scholar] [CrossRef]
  39. Yu, L.; Li, Y.P.; Huang, G.H. Planning municipal-scale mixed energy system for stimulating renewable energy under multiple uncertainties—The City of Qingdao in Shandong Province, China. Energy 2019, 166 , 1120–1133. [Google Scholar] [CrossRef]
  40. Eichler, U.; Brändle, M.; Sauer, J. Predicting Absolute and Site Specific Acidities for Zeolite Catalysts by a Combined Quantum Mechanics/Interatomic Potential Function Approach. J. Phys. Chem. B 2002, 101 , 10035–10050. [Google Scholar] [CrossRef]
  41. Zurek, E.; Grochala, W. Predicting crystal structures and properties of matter under extreme conditions via quantum mechanics: The pressure is on. Phys. Chem. Chem. Phys. 2015, 17 , 2917–2934. [Google Scholar] [CrossRef] [PubMed]
  42. Fischer, C.C.; Tibbetts, K.J.; Morgan, D.; Ceder, G. Predicting crystal structure by merging data mining with quantum mechanics. Nat. Mater. 2006, 5 , 641. [Google Scholar] [CrossRef] [PubMed]
  43. Ceder, G.; Morgan, D.; Fischer, C.; Tibbetts, K.; Curtarolo, S. Data-mining-driven quantum mechanics for the prediction of structure. MRS Bull. 2006, 31 , 981–985. [Google Scholar] [CrossRef]
  44. Kim, H.; Stumpf, A.; Kim, W. Analysis of an energy efficient building design through data mining approach. Autom. Constr. 2011, 20 , 37–43. [Google Scholar] [CrossRef]
  45. Fan, C.; Xiao, F.; Wang, S. Development of prediction models for next-day building energy consumption and peak power demand using data mining techniques. Appl. Energy 2014, 127 , 1–10. [Google Scholar] [CrossRef]
  46. Prakash Maran, J.; Priya, B. Comparison of response surface methodology and artificial neural network approach towards efficient ultrasound-assisted biodiesel production from muskmelon oil. Ultrason. Sonochem. 2015, 23 , 192–200. [Google Scholar] [CrossRef] [PubMed]
  47. Huang, S.-M.; Hung, T.-H.; Liu, Y.-C.; Kuo, C.-H.; Shieh, C.-J. Green Synthesis of Ultraviolet Absorber 2-Ethylhexyl Salicylate: Experimental Design and Artificial Neural Network Modeling. Catalysts 2017, 7 , 342. [Google Scholar] [CrossRef]
  48. Li, H.; Zhang, Z. Mining the intrinsic trends of CO2 solubility in blended solutions. J. CO2 Util. 2018, 26 , 496–502. [Google Scholar] [CrossRef]
  49. Zhang, Z.; Li, H.; Chang, H.; Pan, Z.; Luo, X. Machine Learning Predictive Framework for CO2 Thermodynamic Properties in Solution. J. CO2 Util. 2018, 26 , 152–159. [Google Scholar] [CrossRef]
  50. Abdi-Khanghah, M.; Bemani, A.; Naserzadeh, Z.; Zhang, Z. Prediction of solubility of N-alkanes in supercritical CO2 using RBF-ANN and MLP-ANN. J. CO2 Util. 2018. [Google Scholar] [CrossRef]
  51. Soroush, E.; Shahsavari, S.; Mesbah, M.; Rezakazemi, M.; Zhang, Z. A robust predictive tool for estimating CO2 solubility in potassium based amino acid salt solutions. Chin. J. Chem. Eng. 2018, 26 , 740–746. [Google Scholar] [CrossRef]
  52. Günay, M.E.; Türker, L.; Tapan, N.A. Decision tree analysis for efficient CO2 utilization in electrochemical systems. J. CO2 Util. 2018, 28 , 83–95. [Google Scholar] [CrossRef]
  53. Günay, M.E.; Yildirim, R. Neural network analysis of selective CO oxidation over copper-based catalysts for knowledge extraction from published data in the literature. Ind. Eng. Chem. Res. 2011, 50 , 12488–12500. [Google Scholar] [CrossRef]
  54. Davran-Candan, T.; Günay, M.E.; Yildirim, R. Structure and activity relationship for CO and O2 adsorption over gold nanoparticles using density functional theory and artificial neural networks. J. Chem. Phys. 2010, 132 , 174113. [Google Scholar] [CrossRef] [PubMed]
  55. Hautier, G.; Fischer, C.C.; Jain, A.; Mueller, T.; Ceder, G. Finding natures missing ternary oxide compounds using machine learning and density functional theory. Chem. Mater. 2010, 22 , 3762–3767. [Google Scholar] [CrossRef]
  56. Li, H.; Shin, K.; Henkelman, G. Effects of Ensembles, Ligand, and Strain on Adsorbate Binding to Alloy Surfaces. J. Chem. Phys. 2018, 149 , 174705. [Google Scholar] [CrossRef] [PubMed]
  57. Li, H.; Luo, L.; Kunal, P.; Bonifacio, C.S.; Duan, Z.; Yang, J.C.; Humphrey, S.M.; Crooks, R.M.; Henkelman, G. Oxygen Reduction Reaction on Classically Immiscible Bimetallics: A Case Study of RhAu. J. Phys. Chem. C 2018, 122 , 2712–2716. [Google Scholar] [CrossRef]
  58. Kim, C.; Chandrasekaran, A.; Huan, T.D.; Das, D.; Ramprasad, R. Polymer Genome: A Data-Powered Polymer Informatics Platform for Property Predictions. J. Phys. Chem. C 2018, 122 , 17575–17585. [Google Scholar] [CrossRef]
  59. Graser, J.; Kauwe, S.K.; Sparks, T.D. Machine Learning and Energy Minimization Approaches for Crystal Structure Predictions: A Review and New Horizons. Chem. Mater. 2018, 30 , 3601–3612. [Google Scholar] [CrossRef]
  60. Mansouri Tehrani, A.; Oliynyk, A.O.; Parry, M.; Rizvi, Z.; Couper, S.; Lin, F.; Miyagi, L.; Sparks, T.D.; Brgoch, J. Machine Learning Directed Search for Ultraincompressible, Superhard Materials. J. Am. Chem. Soc. 2018, 140 , 9844–9853. [Google Scholar] [CrossRef] [PubMed]
  61. Yang, Y.; Kang, L.; Li, H. Enhancement of photocatalytic hydrogen production of BiFeO3 by Gd3+ doping. Ceram. Int. 2018, 45 , 8017–8022. [Google Scholar] [CrossRef]
  62. Duan, C.; Huo, J.; Li, F.; Yang, M.; Xi, H. Ultrafast room-temperature synthesis of hierarchically porous metal–organic frameworks by a versatile cooperative template strategy. J. Mater. Sci. 2018, 53 , 16276–16287. [Google Scholar] [CrossRef]
  63. Duan, C.; Li, F.; Xiao, J.; Liu, Z.; Li, C.; Xi, H. Rapid room-temperature synthesis of hierarchical porous zeolitic imidazolate frameworks with high space-time yield. Sci. China Mater. 2017, 60 , 1205–1214. [Google Scholar] [CrossRef]
  64. Yin, K.; Chu, D.; Dong, X.; Wang, C.; Duan, J.A.; He, J. Femtosecond laser induced robust periodic nanoripple structured mesh for highly efficient oil-water separation. Nanoscale 2017, 9 , 14229–14235. [Google Scholar] [CrossRef] [PubMed]
  65. Wang, K.; Pang, J.; Li, L.; Zhou, S.; Li, Y.; Zhang, T. Synthesis of hydrophobic carbon nanotubes/reduced graphene oxide composite films by flash light irradiation. Front. Chem. Sci. Eng. 2018, 12 , 376–382. [Google Scholar] [CrossRef]
  66. Kai, W.; Li, L.; Lan, Y.; Dong, P.; Xia, G. Application Research of Chaotic Carrier Frequency Modulation Technology in Two-Stage Matrix Converter. Math. Probl. Eng. 2019, 2019 , 8. [Google Scholar] [CrossRef]
  67. Kai, W.; Shengzhe, Z.; Yanting, Z.; Jun, R.; Liwei, L.; Yong, L. Synthesis of Porous Carbon by Activation Method and its Electrochemical Performance. Int. J. Electrochem. Sci. 2018, 13 , 10766–10773. [Google Scholar] [CrossRef]
  68. Duan, C.; Cao, Y.; Hu, L.; Fu, D.; Ma, J. Synergistic effect of TiF3 on the dehydriding property of α-AlH3 nano-composite. Mater. Lett. 2019, 238 , 254–257. [Google Scholar] [CrossRef]
  69. Duan, C.W.; Hu, L.X.; Ma, J.L. Ionic liquids as an efficient medium for the mechanochemical synthesis of α-AlH3 nano-composites. J. Mater. Chem. A 2018, 6 , 6309–6318. [Google Scholar] [CrossRef]
  70. Yin, K.; Yang, S.; Dong, X.; Chu, D.; Gong, X.; Duan, J.-A. Femtosecond laser fabrication of shape-gradient platform: Underwater bubbles continuous self-driven and unidirectional transportion. Appl. Surf. Sci. 2018, 471 , 999–1004. [Google Scholar] [CrossRef]
  71. Yin, K.; Yang, S.; Dong, X.; Chu, D.; Duan, J.A.; He, J. Robust laser-structured asymmetrical PTFE mesh for underwater directional transportation and continuous collection of gas bubbles. Appl. Phys. Lett. 2018, 112 , 243701. [Google Scholar] [CrossRef]
  72. Constantinou, L.; Gani, R. New group contribution method for estimating properties of pure compounds. AIChE J. 1994, 40 , 1697–1710. [Google Scholar] [CrossRef]
  73. Behler, J.; Parrinello, M. Generalized neural-network representation of high-dimensional potential-energy surfaces. Phys. Rev. Lett. 2007, 98 , 146401. [Google Scholar] [CrossRef] [PubMed]
  74. Kalogirou, S.A. Optimization of solar systems using artificial neural-networks and genetic algorithms. Appl. Energy 2004, 77 , 383–405. [Google Scholar] [CrossRef]
  75. Kumar, M.; Husian, M.; Upreti, N.; Gupta, D. Genetic Algorithm: Review and Application. Int. J. Inf. Technol. Knowl. Manag. 2010, 2 , 451–454. [Google Scholar]
  76. Iba, H.; Aranha, C.C. Adaptation, Learning, and Optimization ; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
  77. Whitley, D. A genetic algorithm tutorial. Stat. Comput. 1994, 4 , 65–85. [Google Scholar] [CrossRef]
  78. Li, H.; Liu, Z.; Liu, K.; Zhang, Z. Predictive Power of Machine Learning for Optimizing Solar Water Heater Performance: The Potential Application of High-Throughput Screening. Int. J. Photoenergy 2017, 2017 , 4194251. [Google Scholar] [CrossRef]
  79. Li, H.; Liu, Z. Performance Prediction and Optimization of Solar Water Heater via a Knowledge-Based Machine Learning Method. In Handbook of Research on Power and Energy System Optimization ; IGI Global: Hershey, PA, USA, 2018; pp. 55–74. [Google Scholar] [Green Version]
  80. Tetko, I.V.; Livingstone, D.J.; Luik, A.I. Neural Network Studies. 1. Comparison of Overfitting and Overtraining. J. Chem. Inf. Comput. Sci. 1995, 35 , 826–833. [Google Scholar] [CrossRef]

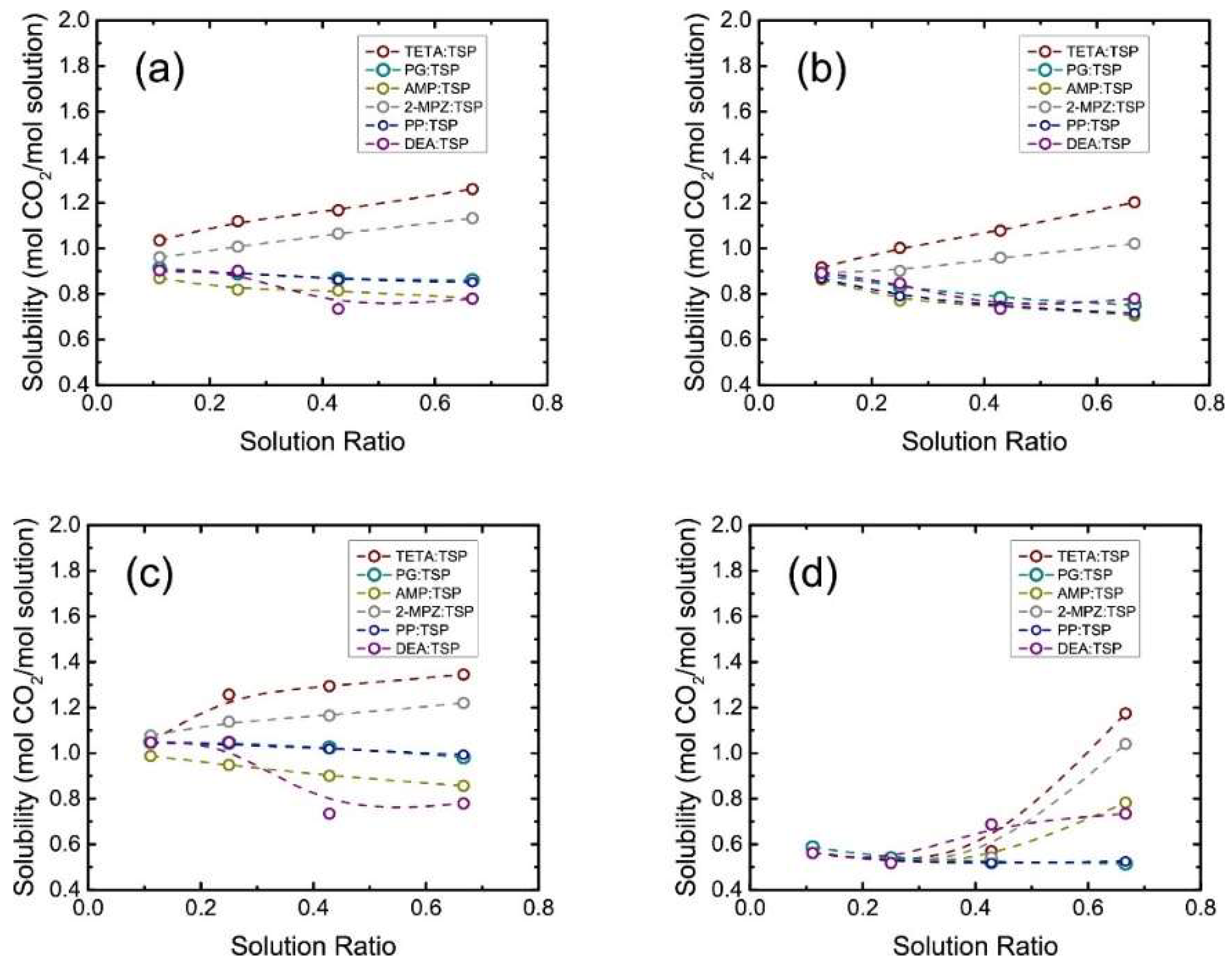
Processes 07 00151 g001 550

Figure 1. Trends in the CO2 capture in blended solutions, predicted by a well-trained general regression neural network model. (a) T = 303 K, P = 14 kPa, C = 2.5 M; (b) T = 323 K, P = 14 kPa, C = 2.5 M; (c) T = 303 K, P = 42 kPa, C = 2.5 M; (d) T = 303 K, P = 14 kPa, C = 1.5 M. T, P, and C represent temperature, CO2 partial pressure, and concentration, respectively. Reproduced with permission from J. CO2 Util. ; published by Elsevier, 2018 [48].

Figure 1. Trends in the CO2 capture in blended solutions, predicted by a well-trained general regression neural network model. (a) T = 303 K, P = 14 kPa, C = 2.5 M; (b) T = 323 K, P = 14 kPa, C = 2.5 M; (c) T = 303 K, P = 42 kPa, C = 2.5 M; (d) T = 303 K, P = 14 kPa, C = 1.5 M. T, P, and C represent temperature, CO2 partial pressure, and concentration, respectively. Reproduced with permission from J. CO2 Util. ; published by Elsevier, 2018 [48].

Processes 07 00151 g001

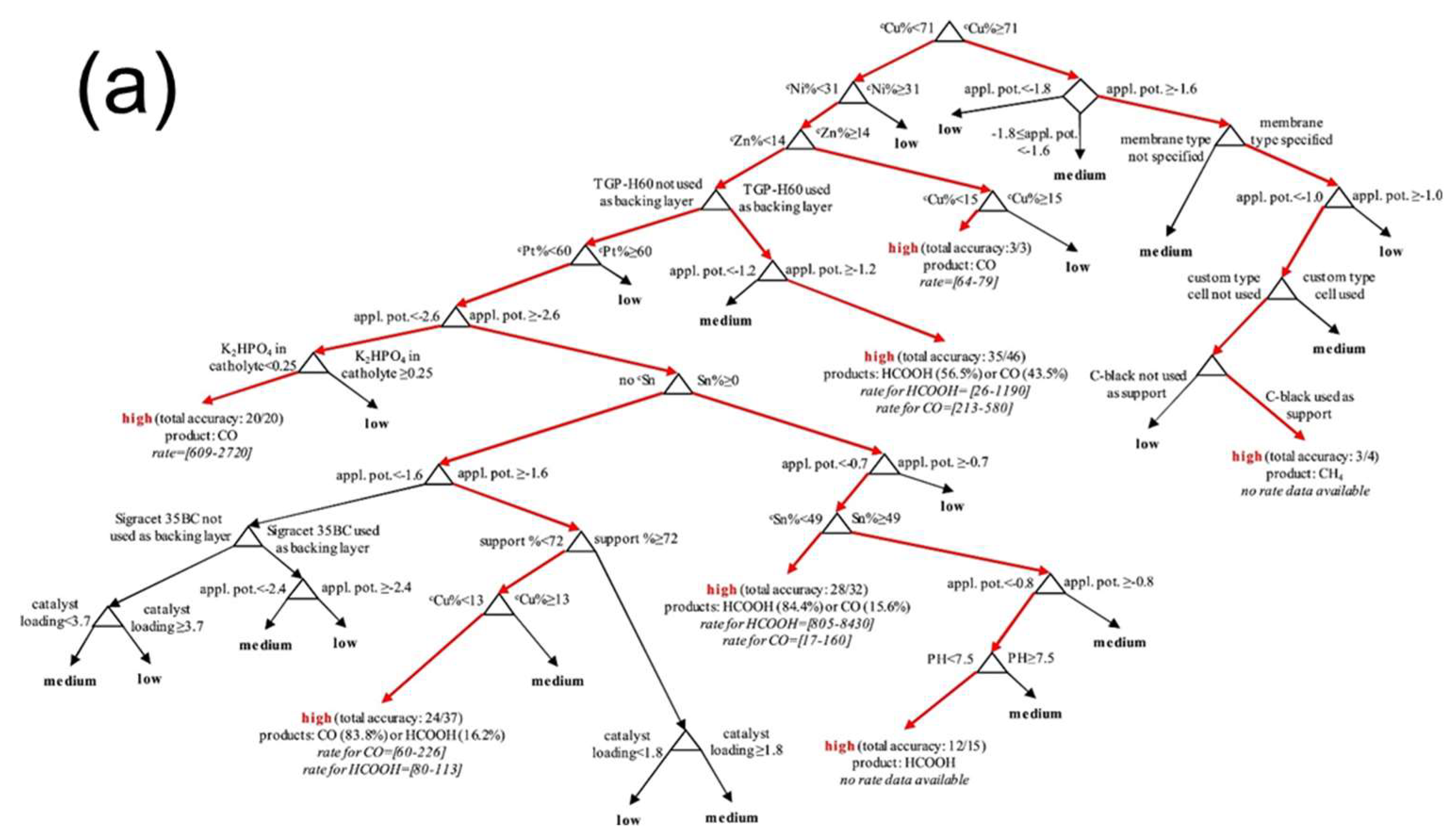
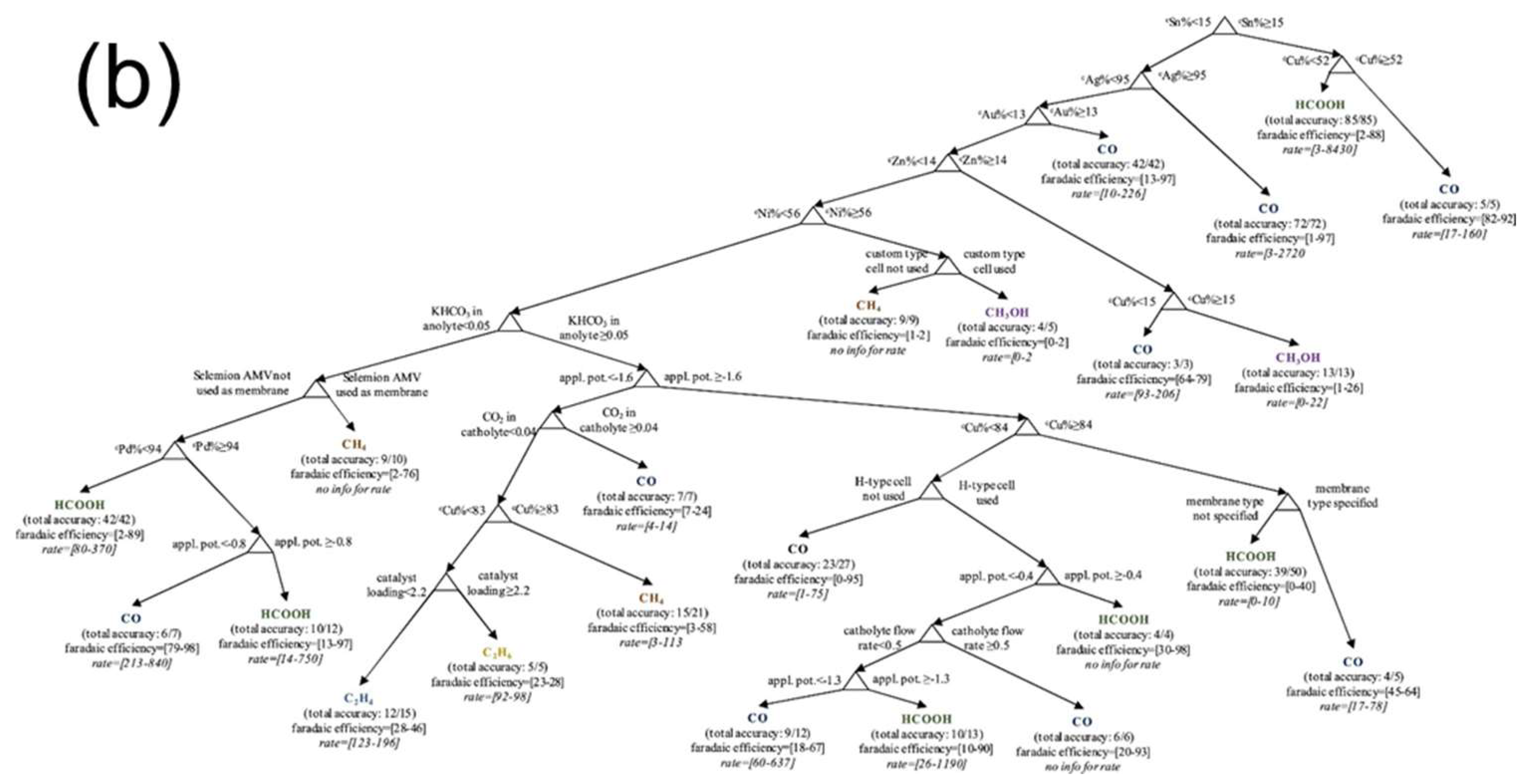
Processes 07 00151 g002a 550 Processes 07 00151 g002b 550

Figure 2. Decision tree analysis for (a) catalysts with maximum faradaic efficiency and (b) catalysts with the highest selective product, for CO2 reduction. Reproduced with permission from J. CO2 Util. ; published by Elsevier, 2018 [52].

Figure 2. Decision tree analysis for (a) catalysts with maximum faradaic efficiency and (b) catalysts with the highest selective product, for CO2 reduction. Reproduced with permission from J. CO2 Util. ; published by Elsevier, 2018 [52].

Processes 07 00151 g002aProcesses 07 00151 g002b

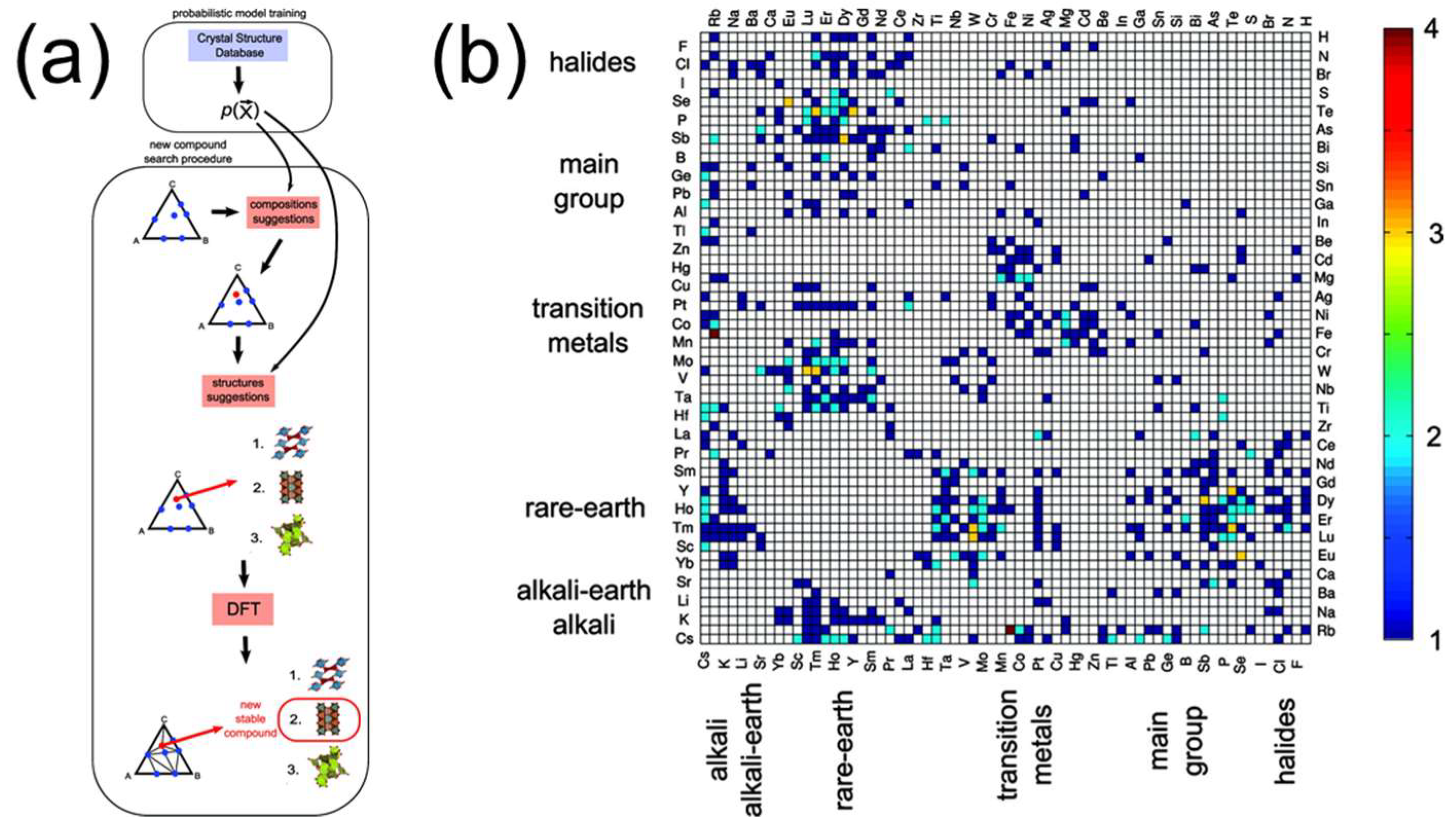
Processes 07 00151 g003 550

Figure 3. (a) A data-mining compound searching procedure proposed by Ceder et al. (b) Distribution of the newly discovered compounds. Reproduced with permission from Chem. Mater .; published by American Chemical Society, 2010 [55].

Figure 3. (a) A data-mining compound searching procedure proposed by Ceder et al. (b) Distribution of the newly discovered compounds. Reproduced with permission from Chem. Mater .; published by American Chemical Society, 2010 [55].

Processes 07 00151 g003

Processes 07 00151 g004 550

Figure 4. A genetic algorithm procedure for optimizing the solar energy systems together with a well-trained artificial neural network model. Reproduced with permission from Appl. Energy ; published by Elsevier, 2004 [74].

Figure 4. A genetic algorithm procedure for optimizing the solar energy systems together with a well-trained artificial neural network model. Reproduced with permission from Appl. Energy ; published by Elsevier, 2004 [74].

Processes 07 00151 g004

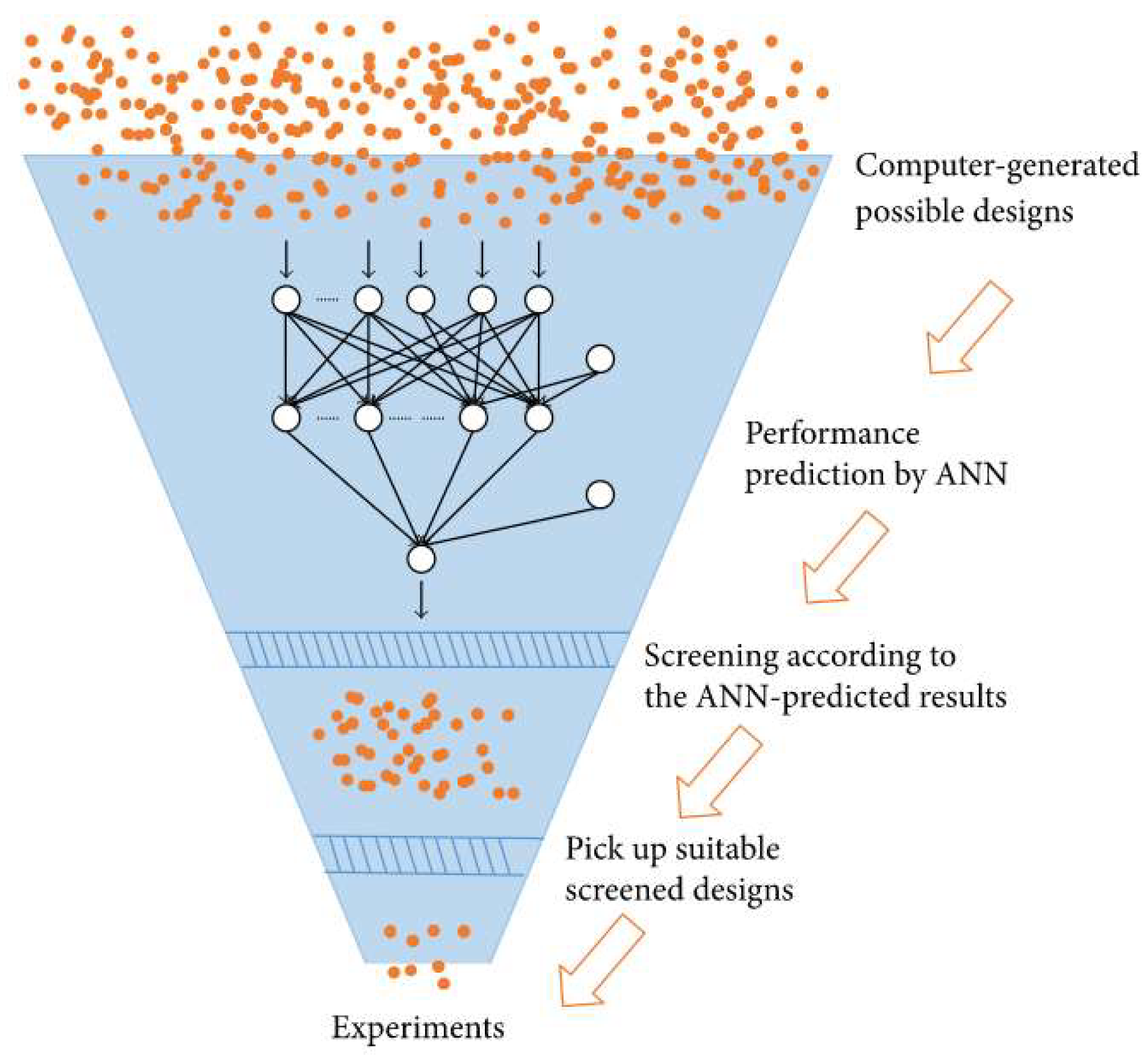
Processes 07 00151 g005 550

Figure 5. A high-throughput screening process for engineering system optimization. Reproduced with permission from Int. J. Photoenergy ; published by Hindawi, 2017 [78].

Figure 5. A high-throughput screening process for engineering system optimization. Reproduced with permission from Int. J. Photoenergy ; published by Hindawi, 2017 [78].

Processes 07 00151 g005

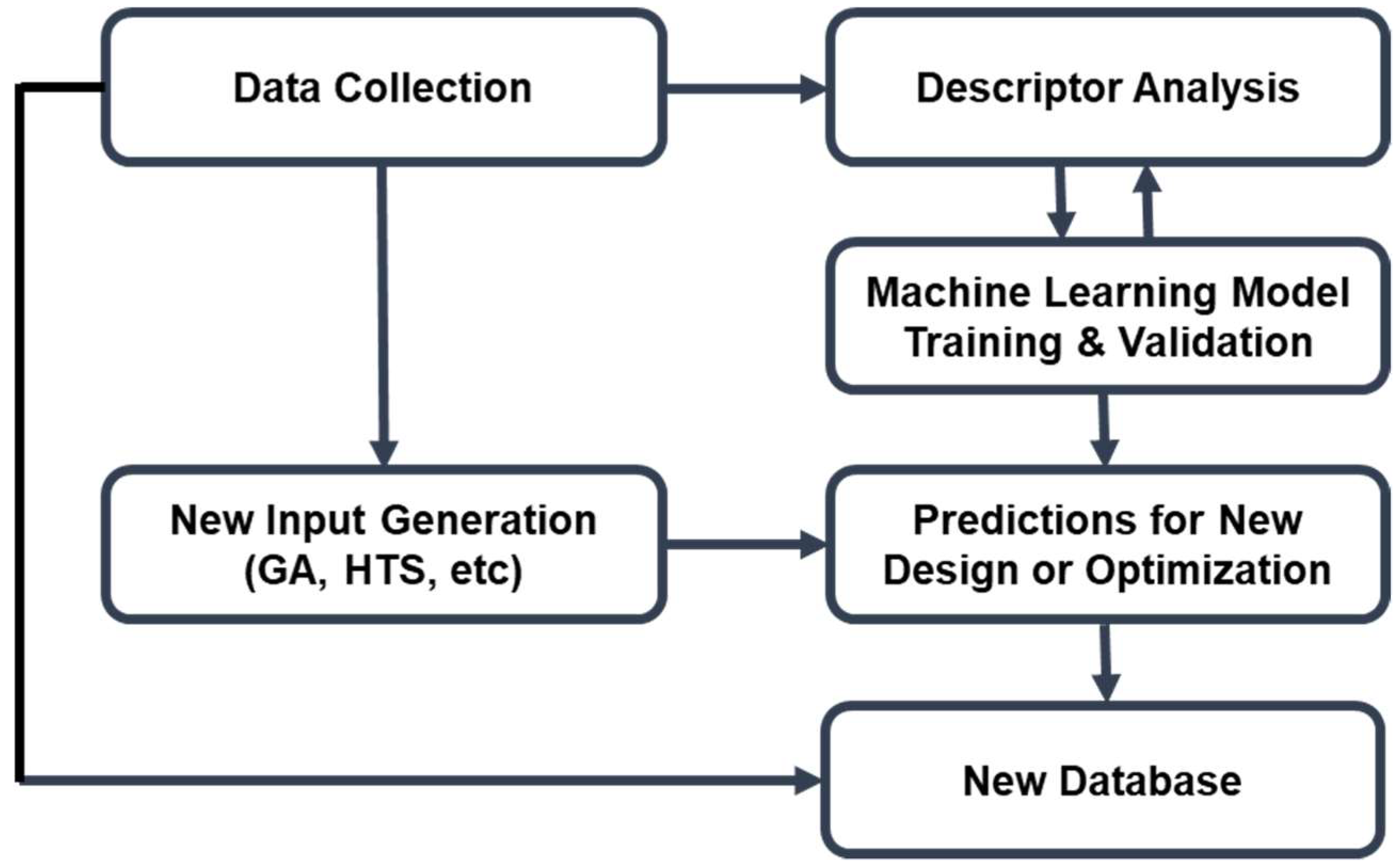
Processes 07 00151 g006 550

Figure 6. Flow chart of the data-mining for processes in natural science and engineering applications.

Figure 6. Flow chart of the data-mining for processes in natural science and engineering applications.

Processes 07 00151 g006


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Share and Cite

MDPI and ACS Style

Li, H.; Zhang, Z.; Zhao, Z.-Z. Data-Mining for Processes in Chemistry, Materials, and Engineering. Processes 2019, 7, 151. https://doi.org/10.3390/pr7030151

AMA Style

Li H, Zhang Z, Zhao Z-Z. Data-Mining for Processes in Chemistry, Materials, and Engineering. Processes. 2019; 7(3):151. https://doi.org/10.3390/pr7030151

Chicago/Turabian Style

Li, Hao, Zhien Zhang, and Zhe-Ze Zhao. 2019. "Data-Mining for Processes in Chemistry, Materials, and Engineering" Processes 7, no. 3: 151. https://doi.org/10.3390/pr7030151

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.